Nothing is so practical as a good theory.
K. Lewin, 1945
Students completing this chapter will
know the structures of the relational model;
understand relational algebra commands;
be able to determine whether a DBMS is completely relational.
The relational model, developed as a result of recognized shortcomings of hierarchical and network DBMSs, was introduced by Codd in 1970. As the major developer, Codd believed that a sound theoretical model would solve many practical problems that might arise.
In another article, Codd expounds the case for adopting the relational over earlier database models. There is a threefold thrust to his argument. First, earlier models forced the programmer to code at a low level of structural detail. As a result, application programs are more complex and took longer to write and debug. Second, no commands were provided for processing multiple records at one time. Earlier models did not provide the set-processing capability of the relational model. The set-processing feature means that queries can be more concisely expressed. Third, the relational model, through a query language such as structured query language (SQL), recognizes the clients’ need to make ad hoc queries. The relational model and SQL permit an IS department to respond rapidly to unanticipated requests. It also meant that analysts could write queries. Thus, Codd’s assertion that the relational model is a practical tool for increasing the productivity of IS departments is well founded.
The productivity increase arises from three of the objectives that drove Codd’s research. The first was to provide a clearly delineated boundary between the logical and physical aspects of database management. Programming should be divorced from considerations of the physical representation of data. Codd labels this the data independence objective. The second objective was to create a simple model that is readily understood by a wide range of analysts and programmers. This communicability objective promotes effective and efficient communication between clients and IS personnel. The third objective was to increase processing capabilities from record-at-a-time to multiple-records-at-a-time—the set-processing objective. Achievement of these objectives means fewer lines of code are required to write an application program, and there is less ambiguity in client-analyst communication.
The relational model has three major components:
Data structures
Integrity rules
Operators used to retrieve, derive, or modify data
Like most theories, the relational model is based on some key structures or concepts. We need to understand these in order to understand the theory.
A domain is a set of values all of the same data type. For example, the domain of nation name is the set of all possible nation names. The domain of all stock prices is the set of all currency values in, say, the range $0 to $10,000,000. You can think of a domain as all the legal values of an attribute.
In specifying a domain, you need to think about the smallest unit of data for an attribute defined on that domain. In Chapter 8, we discussed how a candidate attribute should be examined to see whether it should be segmented (e.g., we divide name into first name, other name, and last name, and maybe more). While it is unlikely that name will be a domain, it is likely that there will be a domain for first name, last name, and so on. Thus, a domain contains values that are in their atomic state; they cannot be decomposed further.
The practical value of a domain is to define what comparisons are permissible. Only attributes drawn from the same domain should be compared; otherwise it is a bit like comparing bananas and strawberries. For example, it makes no sense to compare a stock’s PE ratio to its price. They do not measure the same thing; they belong to different domains. Although the domain concept is useful, it is rarely supported by relational model implementations.
A relation is a table of n columns (or attributes) and m rows (or tuples). Each column has a unique name, and all the values in a column are drawn from the same domain. Each row of the relation is uniquely identified. The order of columns and rows is immaterial.
The cardinality of a relation is its number of rows. The degree
of a relation is the number of columns. For example, the relation nation
(see the following figure) is of degree 3 and has a cardinality of 4.
Because the cardinality of a relation changes every time a row is added
or deleted, you can expect cardinality to change frequently. The degree
changes if a column is added to a relation, but in terms of relational
theory, it is considered to be a new relation. So, only a relation’s
cardinality can change.
A relational database with tables nation and stock
| *natcode | natname | exchrate |
|---|---|---|
| AUS | Australia | 0.46 |
| IND | India | 0.0228 |
| UK | United Kingdom | 1 |
| USA | United States | 0.67 |
| *stkcode | stkfirm | stkprice | stkqty | stkdiv | stkpe | natcode |
|---|---|---|---|---|---|---|
| FC | Freedonia Copper | 27.5 | 10,529 | 1.84 | 16 | UK |
| PT | Patagonian Tea | 55.25 | 12,635 | 2.5 | 10 | UK |
| AR | Abyssinian Ruby | 31.82 | 22,010 | 1.32 | 13 | UK |
| SLG | Sri Lankan Gold | 50.37 | 32,868 | 2.68 | 16 | UK |
| ILZ | Indian Lead & Zinc | 37.75 | 6,390 | 3 | 12 | UK |
| BE | Burmese Elephant | 0.07 | 154,713 | 0.01 | 3 | UK |
| BS | Bolivian Sheep | 12.75 | 231,678 | 1.78 | 11 | UK |
| NG | Nigerian Geese | 35 | 12,323 | 1.68 | 10 | UK |
| CS | Canadian Sugar | 52.78 | 4,716 | 2.5 | 15 | UK |
| ROF | Royal Ostrich Farms | 33.75 | 1,234,923 | 3 | 6 | UK |
| MG | Minnesota Gold | 53.87 | 816,122 | 1 | 25 | USA |
| GP | Georgia Peach | 2.35 | 387,333 | 0.2 | 5 | USA |
| NE | Narembeen Emu | 12.34 | 45,619 | 1 | 8 | AUS |
| QD | Queensland Diamond | 6.73 | 89,251 | 0.5 | 7 | AUS |
| IR | Indooroopilly Ruby | 15.92 | 56,147 | 0.5 | 20 | AUS |
| BD | Bombay Duck | 25.55 | 167,382 | 1 | 12 | IN |
A relational database is a collection of relations or tables. A
distinguishing feature of the relational model, is that there are no explicit linkages between tables. Tables are linked by common columns drawn on the same
domain; thus, the portfolio database (see the preceding tables) consists
of tables stock and nation. The 1:m relationship between the two
tables is represented by the column natcode that is common to both
tables. Note that the two columns need not have the same name, but they
must be drawn on the same domain so that comparison is possible. In the
case of an m:m relationship, while a new table must be created to
represent the relationship, the principle of linking tables through
common columns on the same domain remains in force.
A relation’s primary key is its unique identifier; for example, the
primary key of nation is natcode. As you already know, a primary key
can be a composite of several columns. The primary key guarantees that
each row of a relation can be uniquely addressed.
In some situations, there may be several attributes, known as candidate
keys, that are potential primary keys. Column natcode is unique in the
nation relation, for example. We also can be fairly certain that two
nations will not have the same name. Therefore, nation has multiple
candidate keys: natcode and natname.
When there are multiple candidate keys, one is chosen as the primary
key, and the remainder are known as alternate keys. In this case, we
selected natcode as the primary key, and natname is an alternate
key.
The foreign key is an important concept of the relational model. It is the way relationships are represented and can be thought of as the glue that holds a set of tables together to form a relational database. A foreign key is an attribute (possibly composite) of a relation that is also a primary key of a relation. The foreign key and primary key may be in different relations or the same relation, but both keys must be drawn from the same domain.
The integrity section of the relational model consists of two rules. The entity integrity rule ensures that each instance of an entity described by a relation is identifiable in some way. Its implementation means that each row in a relation can be uniquely distinguished. The rule is
No component of the primary key of a relation may be null.
Null in this case means that the component cannot be undefined or
unknown; it must have a value. Notice that the rule says “component of a
primary key.” This means every part of the primary key must be known. If
a portion of the key cannot be defined, it implies that the particular entity it
describes cannot be defined. In practical terms, it means you cannot add
a nation to nation unless you also define a value for natcode.
The definition of a foreign key implies that there is a corresponding primary key. The referential integrity rule ensures that this is the case. It states
A database must not contain any unmatched foreign key values.
Simply, this rule means that you cannot define a foreign key without
first defining its matching primary key. In practical terms, it would
mean you could not add a Canadian stock to the stock relation without
first creating a row in nation for Canada.
Notice that the concepts of foreign key and referential integrity are intertwined. There is not much sense in having foreign keys without having the referential integrity rule. Permitting a foreign key without a corresponding primary key means the relationship cannot be determined. Note that the referential integrity rule does not imply a foreign key cannot be null. There can be circumstances where a relationship does not exist for a particular instance, in which case the foreign key is null.
There are four approaches to manipulating relational tables, and you are already familiar with SQL, the major method.
Query-by-example (QBE), which describes a general class of graphical interfaces to a relational database to make it easier to write queries, is also commonly used. Less widely used manipulation languages are relational algebra and relational calculus. These languages are briefly discussed, with some attention given to relational algebra in the next section and SQL in the following chapter.
Query-by-example (QBE) is not a standard, and each vendor implements
the idea differently. The general principle is to enable those with
limited SQL skills to interrogate a relational database. Thus, the
analyst might select tables and columns using drag and drop or by
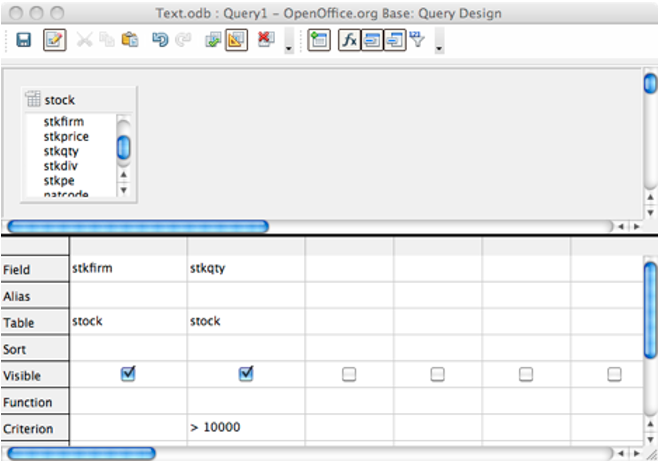
clicking a button. The following screen shot shows the QBE interface to
LibreOffice, which is very similar to that of MS Access. It shows
selection of the stock table and two of its columns, as well as a
criterion for stkqty. QBE commands are translated to SQL prior to
execution, and many systems allow you to view the generated SQL. This
can be handy. You can use QBE to generate a portion of the SQL for a
complex query and then edit the generated code to fine-tune the query.
Query-by-example with LibreOffice
Relational algebra has a set of operations similar to traditional algebra (e.g., add and multiply) for manipulating tables. Although relational algebra can be used to resolve queries, it is seldom employed, because it requires you to specify both what you want and how to get it. That is, you have to specify the operations on each table. This makes relational algebra more difficult to use than SQL, where the focus is on specifying what is wanted.
Relational calculus overcomes some of the shortcomings of relational algebra by concentrating on what is required. In other words, there is less need to specify how the query will operate. Relational calculus is classified as a nonprocedural language, because you do not have to be overly concerned with the procedures by which a result is determined.
Unfortunately, relational calculus can be difficult to learn, and as a result, language designers developed SQL and QBE, which are nonprocedural and more readily mastered. You have already gained some skills in SQL. Although QBE is generally easier to use than SQL, IS professionals need to master SQL for two reasons. First, SQL is frequently embedded in other programming languages, a feature not available with QBE. Second, it is very difficult, or impossible, to express some queries in QBE (e.g., divide). Because SQL is important, it is the focus of the next chapter.
The relational model includes a set of operations, known as relational algebra, for manipulating relations. Relational algebra is a standard for judging data retrieval languages. If a retrieval language, such as SQL, can be used to express every relational algebra operator, it is said to be relationally complete.
Relational algebra operators
| Operator | Description |
|---|---|
| Restrict | Creates a new table from specified rows of an existing table |
| Project | Creates a new table from specified columns of an existing table |
| Product | Creates a new table from all the possible combinations of rows of two existing tables |
| Union | Creates a new table containing rows appearing in one or both tables of two existing tables |
| Intersect | Creates a new table containing rows appearing in both tables of two existing tables |
| Difference | Creates a new table containing rows appearing in one table but not in the other of two existing tables |
| Join | Creates a new table containing all possible combinations of rows of two existing tables satisfying the join condition |
| Divide | Creates a new table containing xi such that the pair (xi, yi) exists in the first table for every yi in the second table |
There are eight relational algebra operations that can be used with either one or two relations to create a new relation. The assignment operator (:=) indicates the name of the new relation. The relational algebra statement to create relation A, the union of relations B and C, is expressed as
A := B UNION C
Before we begin our discussion of each of the eight operators, note that the first two, restrict and project, operate on a single relation and the rest require two relations.
Restrict extracts specified rows from a single relation. It takes a horizontal slice through a relation.
Product creates a new relation from all possible combinations of rows in two other relations. It is sometimes called TIMES or MULTIPLY. The relational command to create the product of two tables is
The operation of product is illustrated in the following figure, which shows the result of A TIMES B.
Relational operator product
| A | B | ||||
|---|---|---|---|---|---|
| V | W | X | Y | Z | |
| v1 | w1 | x1 | y1 | z1 | |
| v2 | w2 | x2 | y2 | z2 | |
| v3 | w3 |
A TIMES B
| V | W | X | Y | Z |
|---|---|---|---|---|
| v1 | w1 | x1 | y1 | z1 |
| v1 | w1 | x2 | y2 | z2 |
| v2 | w2 | x1 | y1 | z1 |
| v2 | w2 | x2 | y2 | z2 |
| v3 | w3 | x1 | y1 | z1 |
| v3 | w3 | x2 | y2 | z2 |
The union of two relations is a new relation containing all rows appearing in one or both relations. The two relations must be union compatible, which means they have the same column names, in the same order, and drawn on the same domains. Duplicate rows are automatically eliminated—they must be, or the relational model is no longer satisfied. The relational command to create the union of two tables is
Union is illustrated in the following figure. Notice that corresponding columns in tables A and B have the same names. While the sum of the number of rows in relations A and B is five, the union contains four rows, because one row (x2, y2 ) is common to both relations.
Relational operator union
| A | B | |||
|---|---|---|---|---|
| X | Y | X | Y | |
| x1 | y1 | x2 | y2 | |
| x2 | y2 | x4 | y4 | |
| x3 | y3 |
A UNION B
| X | Y |
|---|---|
| x1 | y1 |
| x2 | y2 |
| x3 | y3 |
| x4 | y4 |
The intersection of two relations is a new relation containing all rows appearing in both relations. The two relations must be union compatible. The relational command to create the intersection of two tables is
The result of A INTERSECT B is one row, because only one row (x2, y2) is common to both relations A and B.
Relational operator intersect
| A | B | |||
|---|---|---|---|---|
| X | Y | X | Y | |
| x1 | y1 | x2 | y2 | |
| x2 | y2 | x4 | y4 | |
| x3 | y3 |
A INTERSECT B
| X | Y |
|---|---|
| x2 | y2 |
The difference between two relations is a new relation containing all rows appearing in the first relation but not in the second. The two relations must be union compatible. The relational command to create the difference between two tables is
The result of A MINUS B is two rows (see the following figure). Both of these rows are in relation A but not in relation B. The row containing (x1, y2) appears in both A and B and thus is not in A MINUS B.
Relational operator difference
| A | B | |||
|---|---|---|---|---|
| X | Y | X | Y | |
| x1 | y1 | x2 | y2 | |
| x2 | y2 | x4 | y4 | |
| x3 | y3 |
A MINUS B
| X | Y |
|---|---|
| x1 | y1 |
| x3 | y3 |
Join creates a new relation from two relations for all combinations of rows satisfying the join condition. The general format of join is
where theta can be =, <>, >, >=, <, or <=.
The following figure illustrates A JOIN B WHERE W = Z, which is an equijoin because theta is an equals sign. Tables A and B are matched when values in columns W and Z in each relation are equal. The matching columns should be drawn from the same domain. You can also think of join as a product followed by restrict on the resulting relation.
Relational operator join
| A | B | ||||
|---|---|---|---|---|---|
| V | W | X | Y | Z | |
| v1 | wz1 | x1 | y1 | wz1 | |
| v2 | wz2 | x2 | y2 | wz2 | |
| v3 | wz3 |
A EQUIJOIN B
| V | W | X | Y | Z |
|---|---|---|---|---|
| v1 | wz1 | x1 | y1 | wz1 |
| v3 | wz3 | x2 | y2 | wz3 |
Divide is the hardest relational operator to understand. Divide requires that A and B have a set of attributes, in this case Y, that are common to both relations. Conceptually, A divided by B asks the question, “Is there a value in the X column of A (e.g., x1) that has a value in the Y column of A for every value of y in the Y column of B?” Look first at B, where the Y column has values y1 and y2. When you examine the X column of A, you find there are rows (x1, y1) and (x1, y2). That is, for x1, there is a value in the Y column of A for every value of y in the Y column of B. Thus, the result of the division is a new relation with a single row and column containing the value x1.
Relational operator divide
| A | B | ||
|---|---|---|---|
| X | Y | Y | |
| x1 | y1 | y1 | |
| x1 | y3 | y2 | |
| x1 | y2 | ||
| x2 | y1 | ||
| x3 | y3 |
A DIVIDE B
| X |
|---|
| x1 |
The full set of eight relational operators is not required. As you have already seen, join can be defined in terms of product and restrict. Intersection and divide can also be defined in terms of other commands. Indeed, only five operators are required: restrict, project, product, union, and difference. These five are known as primitives because these are the minimal set of relational operators. None of the primitive operators can be defined in terms of the other operators.
The three components of a relational database system are structures (domains and relations), integrity rules (primary and foreign keys), and a manipulation language (relational algebra). A fully relational database system provides complete support for each of these components. Many commercial systems support SQL but do not provide support for domains. Such systems are not fully relational but are relationally complete.
In 1985, Codd established the 12 commandments of relational database systems (see the following table). In addition to providing some insights into Codd’s thinking about the management of data, these rules can also be used to judge how well a database fits the relational model. The major impetus for these rules was uncertainty in the marketplace about the meaning of “relational DBMS.” Codd’s rules are a checklist for establishing the completeness of a relational DBMS. They also provide a short summary of the major features of the relational DBMS.
Codd’s rules for a relational DBMS
| Rules |
|---|
| The information rule |
| The guaranteed access rule |
| Systematic treatment of null values |
| Active online catalog of the relational model |
| The comprehensive data sublanguage rule |
| The view updating rule |
| High-level insert, update, and delete |
| Physical data independence |
| Logical data independence |
| Integrity independence |
| Distribution independence |
| The nonsubversion rule |
There is only one logical representation of data in a database. All data must appear to be stored as values in a table.
Every value in a database must be addressable by specifying its table name, column name, and the primary key of the row in which it is stored.
There must be a distinct representation for unknown or inappropriate data. This must be unique and independent of data type. The DBMS should handle null data in a systematic way. For example, a zero or a blank cannot be used to represent a null. This is one of the more troublesome areas because null can have several meanings (e.g., missing or inappropriate).
There should be an online catalog that describes the relational model. Authorized users should be able to access this catalog using the DBMS’s query language (e.g., SQL).
There must be a relational language that supports data definition, data manipulation, security and integrity constraints, and transaction processing operations. Furthermore, this language must support both interactive querying and application programming and be expressible in text format. SQL fits these requirements.
The system must support set-at-a-time operations. For example, multiple rows must be updatable with a single command.
Changes to storage representation or access methods will not affect application programs. For example, application programs should remain unimpaired even if a database is moved to a different storage device or an index is created for a table.
Information-preserving changes to base tables will not affect application programs. For instance, no applications should be affected when a new table is added to a database.
Integrity constraints should be part of a database’s definition rather than embedded within application programs. It must be possible to change these constraints without affecting any existing application programs.
Introduction of a distributed DBMS or redistribution of existing distributed data should have no impact on existing applications.
It must not be possible to use a record-at-a-time interface to subvert security or integrity constraints. You should not be able, for example, to write a Java program with embedded SQL commands to bypass security features.
Codd issued an additional higher-level rule, rule 0, which states that a relational DBMS must be able to manage databases entirely through its relational capacities. In other words, a DBMS is either totally relational or it is not relational.
The relational model developed as a result of recognized shortcomings of hierarchical and network DBMSs. Codd created a strong theoretical base for the relational model. Three objectives drove relational database research: data independence, communicability, and set processing. The relational model has domain structures, integrity rules, and operators used to retrieve, derive, or modify data. A domain is a set of values all of the same data type. The practical value of a domain is to define what comparisons are permissible. A relation is a table of n columns and m rows. The cardinality of a relation is its number of rows. The degree of a relation is the number of columns.
A relational database is a collection of relations. The distinguishing feature of the relational model is that there are no explicit linkages between tables. A relation’s primary key is its unique identifier. When there are multiple candidates for the primary key, one is chosen as the primary key and the remainder are known as alternate keys. The foreign key is the way relationships are represented and can be thought of as the glue that binds a set of tables together to form a relational database. The purpose of the entity integrity rule is to ensure that each entity described by a relation is identifiable in some way. The referential integrity rule ensures that you cannot define a foreign key without first defining its matching primary key.
The relational model includes a set of operations, known as relational algebra, for manipulating relations. There are eight operations that can be used with either one or two relations to create a new relation. These operations are restrict, project, product, union, intersect, difference, join, and divide. Only five operators, known as primitives, are required to define all eight relational operations. An SQL statement can be translated to relational algebra and vice versa. If a retrieval language can be used to express every relational algebra operator, it is said to be relationally complete. A fully relational database system provides complete support for domains, integrity rules, and a manipulation language. Codd set forth 12 rules that can be used to judge how well a database fits the relational model. He also added rule 0—a DBMS is either totally relational or it is not relational.
| Alternate key | Join |
| Candidate key | Logical data independence |
| Cardinality | Nonsubversion rule |
| Catalog | Null |
| Communicability objective | Operators |
| Data independence | Physical data independence |
| Data structures | Primary key |
| Data sublanguage rule | Product |
| Degree | Project |
| Difference | Query-by-example (QBE) |
| Distribution independence | Referential integrity |
| Divide | Relational algebra |
| Domain | Relational calculus |
| Entity integrity | Set processing objective |
| Foreign key | Relational database |
| Fully relational database | Relational model |
| Guaranteed access rule | Relationally complete |
| Information rule | Relations |
| Integrity independence | Restrict |
| Integrity rules | Union |
| Intersect | View updating rule |
What reasons does Codd give for adopting the relational model?
What are the major components of the relational model?
What is a domain? Why is it useful?
What are the meanings of cardinality and degree?
What is a simple relational database?
What is the difference between a primary key and an alternate key?
Why do we need an entity integrity rule and a referential integrity rule?
What is the meaning of “union compatible”? Which relational operations require union compatibility?
What is meant by the term “a primitive set of operations”?
What is a fully relational database?
How well does LibreOffice’s database satisfy Codd’s rules.